En la última clase nos dedicamos a ver las especificidades de circuitos que se encontraban en régimen permanente sinusoïdal, trabajamos con circuitos RC y con el concepto de función de red/circuito. Hoy, hemos continuado con la temática pasada, sin embargo conforme vamos avanzando en el temario se puede apreciar que las combinaciones mediante componentes electrónicos (resistores, bobinas, condesadores, generadores, etc.) son infinitas y por lo tanto, hay que desarrollar una estratégia con tal de simplificar.
Partiendo de conceptos que ya conociamos, como la asociación de resistencias (tanto en paralelo como en série) se ha introducido un concepto equivalente que nos será muy útil en los circutos transformados fasoriales, la impedancia [Z].
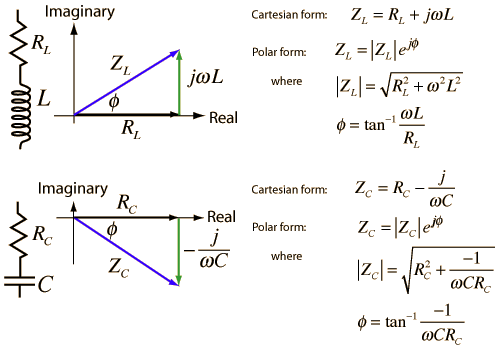 |
| Ejemplos de impedancias en circuitos RL y RC |
Sin entrar más en detalle, hemos de destacar que en esta asignatura trabajaremos con impedancias mediante su forma compleja: Z = a + jb. (Dónde a es la parte real que equivale a la resitencia y b es la parte imaginaria que equivale a la reactancia [X] (suma de ractancias inductivas y capacitivas).

Seguidamente, después de ver ejemplos varios donde se ha visto la utilidad del concepto anterior, hemos tratado por encima conceptos como el de admitancia [Y] (inversa de Z), susceptancia [B] (componente imaginaria de Y), conductancia [G] (componente real de Y)...
Para finalizar, puesto que trabajaremos con números complejos la mayor parte del tiempo se ha acordado trabajar con Sn (dónde Sn=j·w) con tal de reducir errores en caso de olvidarse una j o una w (omega), las cuales aparecerán constantemente.
No hay comentarios:
Publicar un comentario